診断コンテンツの作成方法から活用方法まで、診断のすべてがわかるメディア

そのABテスト、本当に意味ある?統計を活用した正しい手法をご紹介。
マーケティング施策の効果測定に用いられるABテスト。きちんと測定するためには、単純な数値の比較ではなく統計的検定を行う必要があります。本記事では検定手法をわかりやすく解説しつつ、エクセルで簡単に検定を行う方法をご紹介します。
更新日:2023/08/03 公開日:2021/09/16
マーケティング施策の効果を測定するのにはABテストを行っている方は多いと思いますが、クリック率(CTR)やコンバージョン率(CVR)を単純比較しただけでその良し悪しを判定していませんか?
実は数値の大小を見るだけでは、正しく効果測定できているとは言えません。
ABテストの結果を正しく判定するためには「統計」の知識が必要なのです。
そこで今回は、統計を利用した「正しいABテスト」の手法を具体的な事例を交えてご紹介します。
統計と聞くとなんだか難しそうに聞こえるかもしれませんが、なるべく数式を使わずにわかりやすく解説していきますので、ぜひ最後までお読みください。
目次
数値を単純比較するだけではダメな理由
具体的なイメージを持っていただくためにディスプレイ広告などでよく行われる「2つのバナーの効果を比較する」ABテストを考えてみましょう。
同じ期間でバナーAとバナーBをランダムに表示させて、どちらの効果が高いかを調べます。
そのABテストの結果は以下の表のとおりとなりました。
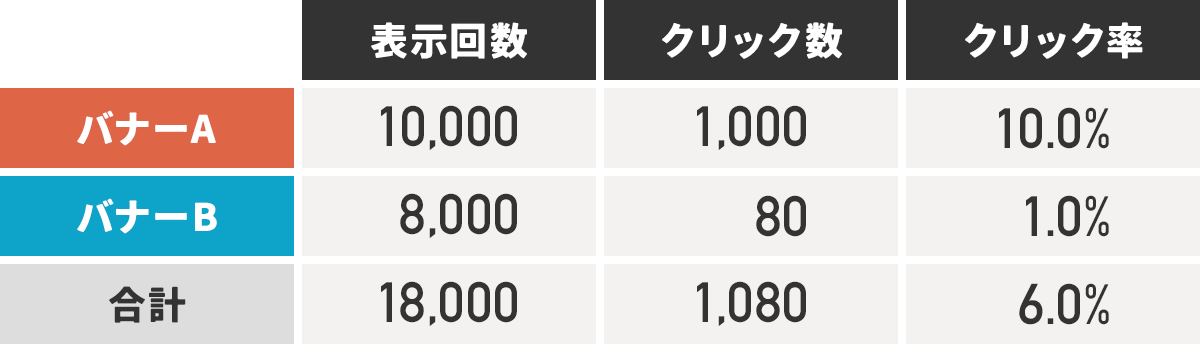
クリック率を見ると、Aの方が9%高いですね。
この場合、明らかに「Aの方が効果が大きい」と言えそうな気がします。
一方、次のような結果が出た場合はどうでしょうか。
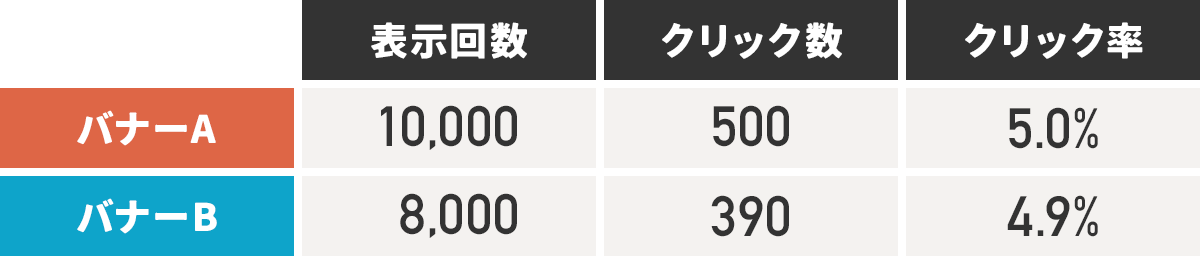
今回もAの方がクリック率は高いですが、その差は0.1%しかありません。
この時も、先ほどと同様に「Aの方が効果が大きい」と自信をもって言えるでしょうか…?
今回たまたまこの結果になっただけで、もう一度同じ条件でテストしたら大小関係がひっくり返る可能性もありそうです。
「いや、0.1%でも高いものは高い!」
と言い切るのは簡単ですが、その判断は主観的なものであり、マーケティング活動で成果を高めていくためには客観的な判断が必要ですよね。
こうしたなんとなくの判断を排除し「本当にAの方が効果が高いのか?」を客観的に判断するためには、「統計的検定」とよばれる手法が必要になります。
ここから統計の具体的な話に入っていきますが、頑張ってついてきてください。

「統計的検定」とは
統計的検定とは、自分の主張の逆となる仮説(帰無仮説)を立てて、その仮説が確率的に起こりえるかを判断する手法です。帰無仮説が起こり得ないと判断されると、仮説が否定(棄却)され、自分の主張となる仮説(対立仮説)が採用されます。
頭の中に「?」の文字がいくつも浮かんでいる方が多いかと思いますので、簡単な例を用いて説明しましょう。
「カレーは飲み物ではない」という主張をしたいときには、まず逆となる帰無仮説「カレーは飲み物である」を設定します。
次に、カレーが飲み物であるとは言えない証拠(粘度が高い、単体で飲むことはない、コップに入れて飲むことはない…など)を用意することで、帰無仮説を棄却(却下)します。
結果として、自分の主張したかった対立仮説の「カレーは飲み物ではない」が採用される、というわけです。
どうしてこんなに面倒なやり方をするのかというと、自分の立てた仮説が正しいことを証明するのは非常に難しいからです。
例えば「全てのカラスは黒い」という命題を証明したい時、ご自身であればどのような方法を考えますか?
この世のカラスを全て調べ上げるか…
この世界にある黒くないものを全て集め、その中にカラスがいないことを調べるか…
いずれにしても現実的ではありませんよね。
対して「全てのカラスは黒い」を否定する場合はどうでしょうか。
この場合は、「1匹でも白いカラスを連れてくる」だけでいいですよね。
このように仮説を否定することは、仮説が正しいことを証明するより遥かに簡単です。
そのため、自分の主張の逆となる仮説(帰無仮説)をわざわざ立ててから、それを否定(棄却)し自分の主張が正しいことを証明しているわけです。
今回のABテストの話に戻りましょう。
先ほどの例で主張したい内容は「バナーA・Bの効果には差がある(≒バナーAの方が効果が大きい)」です。
しかし「差があること」を証明するのは大変です。
差が大きい場合、小さい場合、限りなく小さい場合…など、たくさんのケースを考慮する必要が出てきてしまいます。
そこで統計的検定では先ほどお伝えした通り、自分の主張と対になる仮説(帰無仮説)を立てて、それを否定(棄却)する方法をとります。
今回の帰無仮説は「バナーA・Bの効果に差がない」となります。
この帰無仮説を棄却(却下)するためのエビデンスを見つけることができれば、晴れて「バナーA・Bの効果に差がある」と言えるわけです。
ちなみにこの検定における「差」は「有意差(統計的に意味のある差)」と呼ばれますので
今後ために覚えておくとよいでしょう。
具体的にどうすれば帰無仮説を棄却できるのかは、後ほどご説明します。
ABテストで用いられる手法:カイ二乗検定
統計的検定には様々な種類があるのですが、ABテストで主に用いられるのは「カイ二乗検定」と呼ばれる手法です。
なんだか難しそうな名前ですが、ここでは概要だけお伝えします。
カイ二乗検定は、カテゴリどうしが独立しているかどうかを判断したいときに用います。
ABテストの結果にカイ二乗検定を用いると、バナーの「種類」と「効果」は関係がないのか否かを判定することができるのです。
カイ二乗検定では、カイ二乗値と呼ばれる数値からp値(帰無仮説が起こる確率)を計算します。
p値がこちらで決めた基準(有意水準)よりも小さければ、帰無仮説が起こる確率は低いとみなされ、帰無仮説が棄却され対立する仮説が採用されます。
なお有意水準には、5%(0.05)が採用されることが多いです。
きっとまた頭に「?」が浮かんできたと思いますので、例を見ていきましょう。
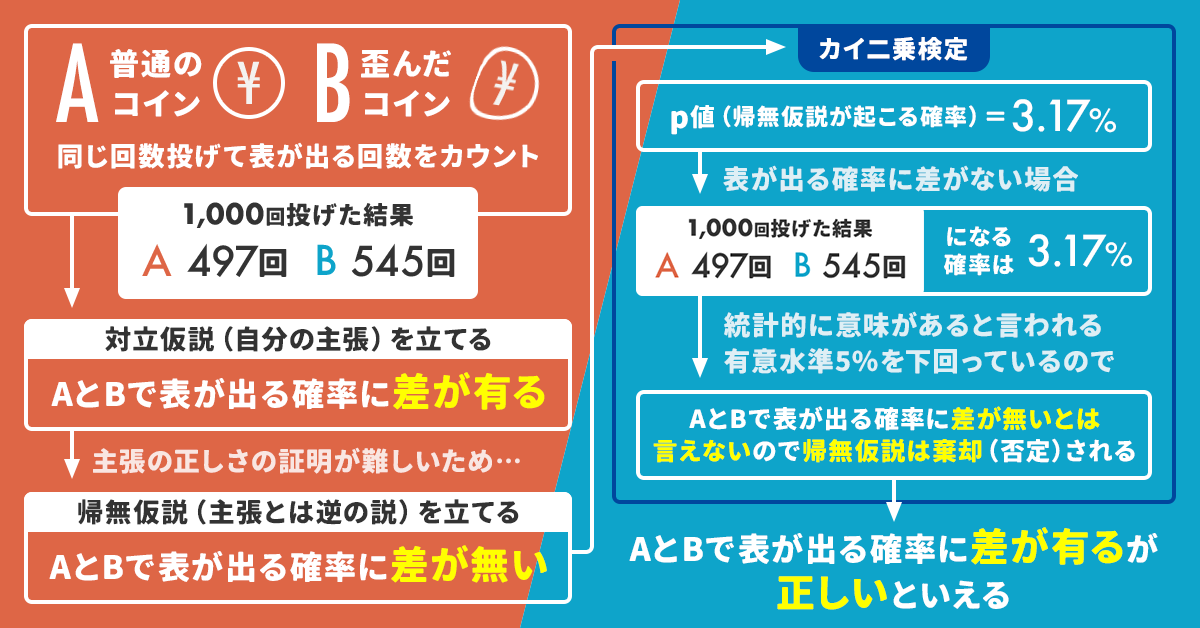
コインAと歪んでいるコインBを投げ、その表と裏が出た数をカウントすることを考えます。
ABともに1000回ずつ投げて、表が出た回数が「A:497回、B:545回」になったとしましょう。
Bのほうが表が出た回数が40回以上も多いので、「コインA・Bの表の出やすさに差がある(≒Bのほうが表が出やすい)」と言えそうです。
これを示すために「コインA・Bの表の出やすさに差はない」という帰無仮説を立てます。
次にp値(帰無仮説が起きる確率)を計算するのですが、上の例で計算すると3.17%となりました。
つまり「もしコインA・Bの表の出やすさに差がないとした時に、1000回投げて表が出た回数がA:497回、B:545回となる可能性」は3.17%しかない(確率がものすごい低い)ということです。
p値が有意水準の5%よりも小さいので、「コインA・Bに差がない」とは考えにくく、帰無仮説を否定(棄却)することができ、「コインA・Bの表の出やすさに差がある」という主張が採用されました。
ここまでの流れをまとめると以下のようになります。
「まだピンとこない…」という人もいるかと思いますが、統計を本質的に理解するのは正直大変です。実際に検定を行いながら少しずつ理解していくようにしましょう。

カイ二乗検定の手順
それでは、ABテストにおけるカイ二乗検定の手順を説明していきます。
エクセルを使えば比較的容易に実施できるので、ご紹介する例を見ながらご自分のPCでも試してみてください。
①データを集計する
まずは当たり前ですが、ABテストを実施してデータを集めます。
ABテストを行う際に気を付けたいのは、以下の3つです。
・比較対象のコンテンツの差異を大きくしすぎない
ABテストの結果に有意な差が見られたとしても、コンテンツの差異が複数箇所あるとどの要素が効果の差に結びついたのか判断できません。バナーであれば文言だけ、色味だけ、あるいは写真だけといった1要素の差異におさめるようにしましょう。
・コンテンツ以外の条件を揃える
コンテンツの差異以外による影響をなるべく排除したいので、他の条件は揃えるようにしましょう。バナーであれば表示場所や表示対象、表示期間を同一にするといった設定が必要です。
・十分なデータ数を用意する
表示回数が少なすぎると誤差が大きくなってしまうため、正しく検定が行えません。
10人中6人がクリックしたのと、1000人中600人がクリックしたのではクリック率は同じ60%ですが、後者の方が信頼できそうですよね。あくまで目安ですが、バナーのABテストであれば最低でも2000回ずつ配信して測定するようにしましょう。
②結果を表にまとめる
ABテストの結果が出たら、わかりやすくするため表にまとめます。
バナーでABテストをした場合だと以下のような形になります。
表①
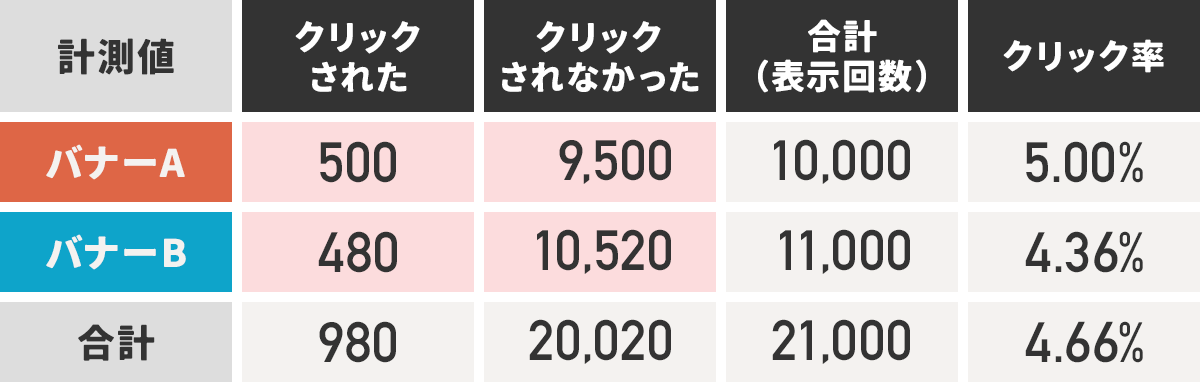
それぞれのバナーがクリックされた回数、クリックされなかった回数を表にまとめてください。
クリック率だけ見ると、バナーAの方が0.64%高いですね。
はたして、バナーAの方が効果が高いといえるのでしょうか…?
③期待値を計算する
次に、期待値を計算します。
期待値をざっくり説明すると「確率を考慮した平均値」です。
例えばサイコロだと各目が出る確率は1/6なので、期待値は
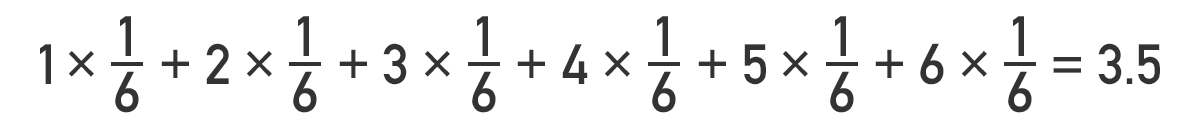
です。
今回は「バナーAとバナーBの効果に差がないと仮定した時、期待される値」を導き出します。
AとBの効果に差がないということは、AとBで「クリックされた」「クリックされなかった」の比が同じということです。
それぞれの合計を見ると「クリックされた」が980回で、「クリックされなかった」が20020回です。
つまり、バナーAでもバナーBでも「クリックされた」と「クリックされなかった」の期待値の比は980:20020になります。
バナーA・Bの各表示回数から期待される「クリックされた」「クリックされなかった」の数値を導き出しましょう。
バナーAがクリックされる回数の期待値は
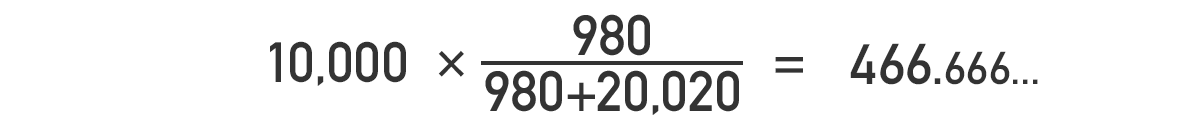
バナーAがクリックされない回数の期待値は
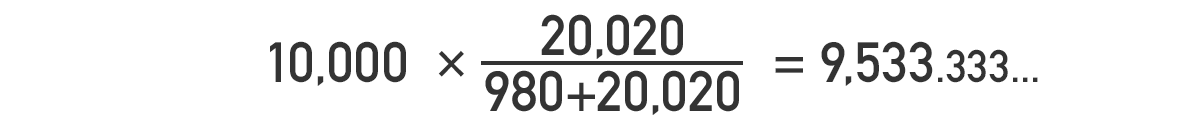
です。
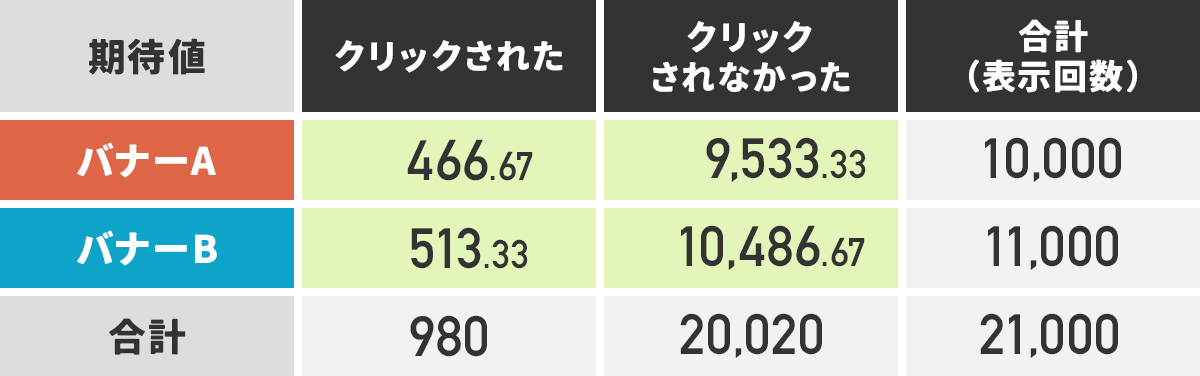
バナーBについても計算すると、以下のようになりました。
表②
④p値を計算する
本来のカイ二乗検定では、ここからカイ二乗値と自由度を計算して統計数値表からp値の範囲を計算して…という作業が必要になります。
しかし今回はそんな難しいことは省略して、エクセルに計算してもらいましょう。
p値、つまり帰無仮説が起こる確率をエクセルで計算するためには、以下の関数を使用します。

計測値の範囲には表①のピンクの箇所、期待値の範囲には表②の緑の箇所を選んでください。
この関数を使って計算すると、p値は「2.9%」と計算できます。
⑤p値と有意水準を比較する
計算して求められたp値と「これより小さければ帰無仮説は棄却できる」という基準値(有意水準)を比較します。
有意水準には5%が用いられることが多いので、今回も5%を採用しましょう。
比較すると「2.9%<5%」となり、帰無仮説の起こる確率は低いということで「バナーAとバナーBの効果には差がない」を棄却できます。
よって対立仮説の「バナーAとバナーBの効果には差がある」が採用され、晴れてバナーAの効果の方が高かったと主張することができました。

まとめ
ここまで、カイ二乗検定を用いたABテストについてご紹介してきました。
数学に馴染みがないと難しく感じるかもしれませんが、本来ABテストはこういった計算が必要になります。
ABテスト以外にも、統計や検定の知識はマーケティングにおいて非常に役立ちます。
データの平均値だけ見ていたところをデータの分布を観察してみると、違う発見があったり、実は思いもよらぬ項目に相関関係があったりします。
統計の知識は効果測定や意思決定において大きな武器となるので、ぜひ勉強してみてください。
想定される活用シーン
ライター:ピクルス スタッフ
マーケティング支援










